pytorch数据批次的大小对模型拟合效果的影响

本次使用大小为 [29995x30] 的数据集进行回归预测，研究设置不同的数据批次对模型拟合效果的影响。

过程：

1、导入数据
2、建立 XGBRegressor() 模型，计算均方误差。
3、建立4个结构相同的深度学习模型，在相同的循环次数下设置不同的批次查看均方误差别，及训练批次和验证批次不同的情况下均方误差的的差别。

导入模块及数据：

import numpy as np import pandas as pd import matplotlib.pyplot as plt import sklearn.preprocessing as ps from sklearn.model_selection import train_test_split from xgboost import XGBRegressor import torch import torch.nn as nn import torch.nn.functional as F import torch.optim as optim from torch.utils.data import TensorDataset from torch.utils.data import DataLoader  data = pd.read_excel("finally_data.xlsx") data.drop(columns='Unnamed: 0',inplace=True) print(data)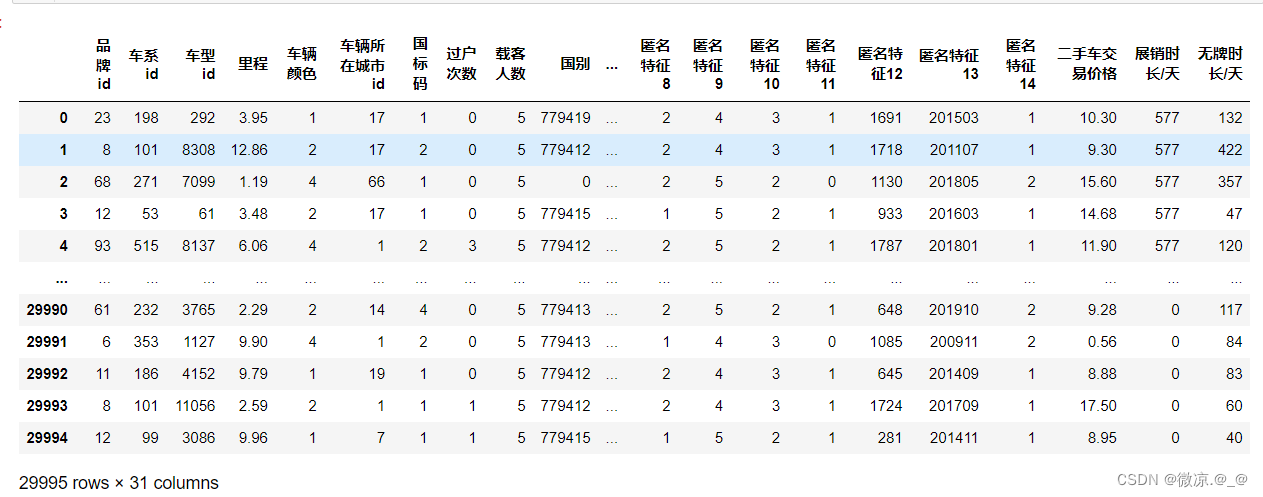 

数据处理

#划分数据和标签 train = data.drop(columns="二手车交易价格") target = data["二手车交易价格"] scale_data = ps.scale(train)#标准化 normalize_data = ps.normalize(train,norm="l1")#归一化 #划分训练集和测试集 xs_train,xs_test,ys_train,ys_test = train_test_split(scale_data,target,test_size=0.2,random_state=666) xn_train,xn_test,yn_train,yn_test = train_test_split(normalize_data,target,test_size=0.2,random_state=666) 

xgboost建模

#标准化后的数据 xgb = XGBRegressor(max_depth=10,learning_rate=0.01,n_estimators=100,random_state=666) xgb.fit(xs_train,ys_train) train_predints = xgb.predict(xs_train) test_predints = xgb.predict(xs_test) print("s:",xgb.score(xs_test,ys_test)) #归一化后的数据 xgb.fit(xn_train,yn_train) train_predintn = xgb.predict(xn_train) test_predintn = xgb.predict(xn_test) print("n",xgb.score(xn_test,yn_test))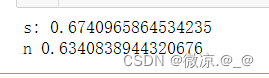 

模型评分

计算误差

#平均误差 def mse(predict,y):     MSE = abs(predict-y).mean()     return MSE #均方误差 def mse2(predict,y):     MSE = ((predict-y)**2).mean()     return MSE     print("平均误差：") train_mess = mse(train_predints,ys_train) test_mess = mse(test_predints,ys_test)  train_mesn = mse(train_predintn,yn_train) test_mesn = mse(test_predintn,yn_test)  print(f"s:训练集：{train_mess} 测试集：{test_mess}") print(f"n:训练集：{train_mesn} 测试集：{test_mesn}")  print("均方误差：") train_mess2 = mse2(train_predints,ys_train) test_mess2 = mse2(test_predints,ys_test)  train_mesn2 = mse2(train_predintn,yn_train) test_mesn2 = mse2(test_predintn,yn_test)  print(f"s:训练集：{train_mess2} 测试集：{test_mess2}") print(f"n:训练集：{train_mesn2} 测试集：{test_mesn2}")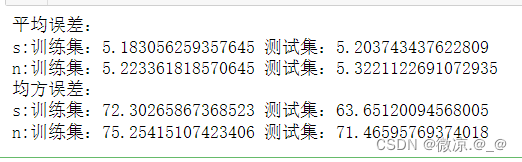 

深度学习模型

#将数据类型转换为tensor txs_train = torch.from_numpy(xs_train).type(torch.float32) tys_train = torch.from_numpy(ys_train.values.reshape(-1,1)).type(torch.float32) txs_test = torch.from_numpy(xs_test).type(torch.float32) tys_test = torch.from_numpy(ys_test.values.reshape(-1,1)).type(torch.float32) #定义批次及设备 sample_train = txs_train.size(0)  sample_test = txs_test.size(0) batch = 64    #最小批次 batch_big = 1024    #中间批次 batch_biggest = sample_train    #最大批次 device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu") 

定义模型及训练

# 模型初始化：方法一 net0_model = nn.Sequential(     nn.Linear(30,60),     nn.ReLU(),     nn.Linear(60,60),     nn.ReLU(),     nn.Linear(60,1))  net0_model.to(device)  #定义损失函数及优化器 loss_function = nn.MSELoss() optimizer = optim.SGD(net0_model.parameters(), lr=0.001)  # 定义训练方法 def train_model(model,sample_train,sample_test,batch,train_datas,train_ys,test_datas,test_ys,optimizer,loss_fun,epoch,device):     model.train()     times_train = sample_train // batch if sample_train % batch == 0 else sample_train // batch + 1     train_loss = 0.0     for i in range(times_train):         start = i * batch         end = start + batch         train_x = train_datas[start:end].to(device)         train_y = train_ys[start:end].to(device)         output = model(train_x)         loss = loss_fun(output,train_y)         train_loss += loss.item()         optimizer.zero_grad()         loss.backward()         optimizer.step()         if i % 10 == 0:             print("split_loss : {:.4f}".format(loss.item()))     print("epoch:{},\ntrain_loss:{:.4f}:".format(epoch,train_loss/times_train))              model.eval()     test_loss = 0.0     times_test = sample_test // batch if sample_test % batch == 0 else sample_test // batch + 1     with torch.no_grad():         for i in range(times_test):             start = i * batch             end = start + batch             test_x = test_datas[start:end].to(device)             test_y = test_ys[start:end].to(device)             predict = model(test_x)             test_loss += loss_fun(predict,test_y).item()         print("test_loss:{:.4f}".format(test_loss/times_test))          #最大批次(全部数据)计算 for epoch in range(100):     train_model(net0_model,sample_train,sample_test,batch_biggest,txs_train,tys_train,txs_test,tys_test,optimizer,loss_function,epoch,device) 

结果

# 模型初始化：方法二 class Model(nn.Module):     def __init__(self):         super(Model,self).__init__()         self.input = nn.Linear(30,60)         self.hidden = nn.Linear(60,60)         self.output = nn.Linear(60,1)          def forward(self,x):         x = F.relu(self.input(x))         x = F.relu(self.hidden(x))         x = self.output(x)                  return x  net1_model = Model() net1_model.to(device) optimizer = optim.SGD(net1_model.parameters(), lr=0.001)  #batch为 1024 时 for epoch in range(100):     train_model(net1_model,sample_train,sample_test,batch_big,txs_train,tys_train,txs_test,tys_test,optimizer,loss_function,epoch,device) 

结果

#采用TensorDataset()和DataLoader()封装数据 x_train_td = TensorDataset(txs_train,tys_train) x_train_dl = DataLoader(x_train_td,batch_size=batch,shuffle=True)  x_test_td = TensorDataset(txs_test,tys_test) x_test_dl = DataLoader(x_test_td,batch_size=batch)  net2_model = Model() net2_model.to(device) optimizer = optim.SGD(net2_model.parameters(), lr=0.001)  #训练批次为64，测试批次为全部数据  for epoch in range(100):     for data,label in x_train_dl:         data,label = data.to(device),label.to(device)         out = net2_model(data)         loss = loss_function(out,label)         optimizer.zero_grad()         loss.backward()         optimizer.step()         print("split_loss:",loss.item())          with torch.no_grad():         txs_train, tys_train = txs_train.to(device), tys_train.to(device)         txs_test, tys_test = txs_test.to(device), tys_test.to(device)         train_all_loss = loss_function(net2_model(txs_train),tys_train).item()         test_all_loss = loss_function(net2_model(txs_test),tys_test).item()         print("epoch:{},train_mse:{:.4f},test_mse:{:.4f}".format(epoch,train_all_loss,test_all_loss)) 

结果

net3_model = Model() net3_model.to(device) optimizer = optim.SGD(net3_model.parameters(), lr=0.001) #训练批次为64，测试批次为64  for epoch in range(100):     times = 0.0     train_all_loss = 0.0     for datas,labels in x_train_dl:         times += 1         datas,labels = datas.to(device),labels.to(device)         train_out = net3_model(datas)         train_loss = loss_function(train_out,labels)         train_all_loss += train_loss.item()         optimizer.zero_grad()         train_loss.backward()         optimizer.step()         print("split_loss:",train_loss.item())          with torch.no_grad():         time = 0.0         test_all_loss = 0.0         for data,label in x_test_dl:             time += 1             data,label = data.to(device),label.to(device)             test_out = net3_model(data)             test_loss = loss_function(test_out,label)             test_all_loss += test_loss.item()         print("epoch:{},train_mse:{:.4f},test_mse:{:.4f}".format(epoch,train_all_loss/times,test_all_loss/time)) 

结果

最终可发现：批次越小整体均方误差越小；训练批次和测试批次相同或不同对整体均方误差的影响不大。